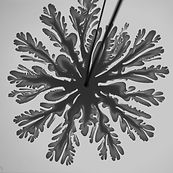
Fluid instabilities
Dendritic patterns from shear-enhanced anisotropy in nematic liquid crystals

Controlling the growth morphology of fluid instabilities is challenging because of their self-amplified and non-linear growth. The viscous fingering instability, which arises when a less viscous fluid displaces a more viscous one, transitions from exhibiting dense-branching growth characterized by repeated tip splitting of the growing fingers to dendritic growth characterized by stable tips in the presence of anisotropy. We controllably induce such a morphology transition by shear-enhancing the anisotropy of nematic liquid crystal solutions. For fast enough flow induced by the finger growth, the intrinsic tumbling behavior of lyotropic chromonic liquid crystals can be suppressed, which results in a flow alignment of the material. This microscopic change in the director field occurs as the viscous torque from the shear flow becomes dominant over the elastic torque from the nematic potential and macroscopically enhances the liquid crystal anisotropy to induce the transition to dendritic growth.
Dendritic patterns from shear-enhanced anisotropy in nematic liquid crystals
Q. Zhang, S. Zhou, R. Zhang, I. Bischofberger, Sci. Adv., 9 (2), eabq6820 (2023)
Structures and topological defects in pressure-driven lyotropic chromonic liquid crystals

Lyotropic chromonic liquid crystals are water-based materials composed of self-assembled cylindrical aggregates. Their behavior under flow is poorly understood, and quantitatively resolving the optical retardance of the flowing liquid crystal has so far been limited by the imaging speed of current polarization-resolved imaging techniques. Here, we employ a single-shot quantitative polarization imaging method, termed polarized shearing interference microscopy, to quantify the spatial distribution and the dynamics of the structures emerging in nematic disodium cromoglycate solutions in a microfluidic channel. We show that pure-twist disclination loops nucleate in the bulk flow over a range of shear rates. These loops are elongated in the flow direction and exhibit a constant aspect ratio that is governed by the nonnegligible splay-bend anisotropy at the loop boundary. The size of the loops is set by the balance between nucleation forces and annihilation forces acting on the disclination. The fluctuations of the pure-twist disclination loops reflect the tumbling character of nematic disodium cromoglycate. Our study, including experiment, simulation, and scaling analysis, provides a comprehensive understanding of the structure and dynamics of pressure-driven lyotropic chromonic liquid crystals and might open new routes for using these materials to control assembly and flow of biological systems or particles in microfluidic devices.
Structures and topological defects in pressure-driven lyotropic chromonic liquid crystals
Q. Zhang, B. Ge, R. Zhang, Z. Yaqoob, P.T.C. So, I. Bischofberger, PNAS, 118, 35, e2108361118 (2021)
Growth morphology and symmetry selection of interfacial instabilities in anisotropic environments

The displacement of a fluid by another less viscous one in a quasi-two dimensional geometry typically leads to complex fingering patterns. In an isotropic system, dense-branching growth arises, which is characterized by repeated tip-splitting of evolving fingers. When anisotropy is present in the interfacial dynamics, the growth morphology changes to dendritic growth characterized by regular structures. We introduce anisotropy by engraving a six-fold symmetric lattice of channels on a Hele-Shaw cell. We show that
the morphology transition in miscible fluids depends not only on the previously reported degree of anisotropy set by the lattice topography, but also on the viscosity ratio between the two fluids. Remarkably, the viscosity ratio and the degree of anisotropy also govern the global features of the dendritic patterns, inducing a systematic change from six-fold towards twelve-fold symmetric dendrites. Varying either control parameter provides a new method to tune the symmetry of complex patterns, which may also have relevance for analogous phenomena of gradient-driven interfacial dynamics, such asdirectional solidification or electrodeposition.
Growth morphology and symmetry selection of interfacial instabilities in anisotropic environments
Q. Zhang, M. A. Amooie, M. Z. Bazant, I. Bischofberger, Soft Matter, 17, 1202 (2021)
Confinement-induced stabilization of the Rayleigh-Taylor instability and transition to the unconfined limit

The prevention of hydrodynamic instabilities can lead to important insights for understanding the instabilities’ underlying dynamics. The Rayleigh-Taylor instability that arises when a dense fluid sinks into and displaces a lighter one is particularly difficult to arrest. By preparing a density inversion between two miscible fluids inside the thin gap separating two flat plates, we create a clean initial stationary interface. Under these conditions, we find that the instability is suppressed below a critical plate spacing. With increasing spacing, the system transitions from the limit of stability where mass diffusion dominates over buoyant forces, through a regime where the gap sets the wavelength of the instability, to the unconfined regime governed by the competition between buoyancy and momentum diffusion. Our study, including experiment, simulation, and linear stability analysis, characterizes all three regimes of confinement and opens new routes for controlling mixing processes.
Criterion for fingering instabilities in colloidal gels

Criterion for instabilities in colloidal gels
T. Divoux, A. Shukla, B. Marsit, Y. Kaloga, I. Bischofberger, Phys. Rev. Lett., 124, 248006 (2020)
We sandwich a colloidal gel between two parallel plates and induce a radial flow by lifting the upper plate at a constant velocity. Two distinct scenarios result from such a tensile test: (i) stable flows during which the gel undergoes a tensile deformation without yielding, and (ii) unstable flows characterized by the radial growth of air fingers into the gel. We show that the unstable regime occurs beyond a critical energy input, independent of the gel’s macroscopic yield stress. This implies a local fluidization of the gel at the tip of the growing fingers and results in the most unstable wavelength of the patterns exhibiting the characteristic scalings of the classical viscous fingering instability. Our work provides a quantitative criterion for the onset of fingering in colloidal gels based on a local shear-induced yielding, in agreement with the delayed failure framework.
Fingering versus stability in the limit of zero interfacial tension

Fingering versus stability in the limit of zero interfacial tension
I. Bischofberger, R. Ramachandran and S. R. Nagel, Nat. Commun. 5:5265 (2014)
Fluid instabilities that mimic animal growth
I. Bischofberger and S. R. Nagel, Phys. Today 69, 70-71 (2016)
The invasion of one fluid into another of higher viscosity in a quasi-two-dimensional geometry typically produces complex fingering patterns. Because interfacial tension suppresses short-wavelength fluctuations, its elimination by using pairs of miscible fluids would suggest an instability producing highly ramified singular structures. Previous studies focused on wavelength selection at the instability onset and overlooked the striking features appearing more globally. Here we investigate the non-linear growth that occurs after the instability has been fully established. We find a rich variety of patterns that are characterized by the viscosity ratio between the inner and the outer fluid, ηin/ηout, as distinct from the most-unstable wavelength, which determines the onset of the instability. As ηin/ηout increases, a regime dominated by long highly-branched fractal fingers gives way to one dominated by blunt stable structures characteristic of proportionate growth. Simultaneously, a central region of complete outer-fluid displacement grows until it encompasses the entire pattern at ηin/ηout ≈ 0.3.
An island of stability in a sea of fingers: emergent global features of the viscous-flow instability

The displacement of a more viscous fluid by a less viscous one in a quasi-two dimensional geometry leads to the formation of complex fingering patterns. This fingering has been characterized by a most unstable wavelength which depends on the viscosity difference between two immiscible fluids and sets the characteristic width of the fingers. How the finger length grows after the instability occurs is an equally important, but previously overlooked, aspect that characterizes the global features of the patterns. Long after the instability onset, once the fingers are growing in a nearly steady-state regime, there is a stable inner region where the outer fluid is completely displaced. We show that the ratio of the finger length to the radius of this stable region depends only on the viscosity ratio of the fluids and is decoupled from the most unstable wavelength.
An island of stability in a sea of fingers: emergent large-scale features of the viscous flow instability
I. Bischofberger, R. Ramachandran, S. R. Nagel, Soft Matter, 11, 7428 (2015)

